Brass Weight vs Case Capacity

[steve4102]

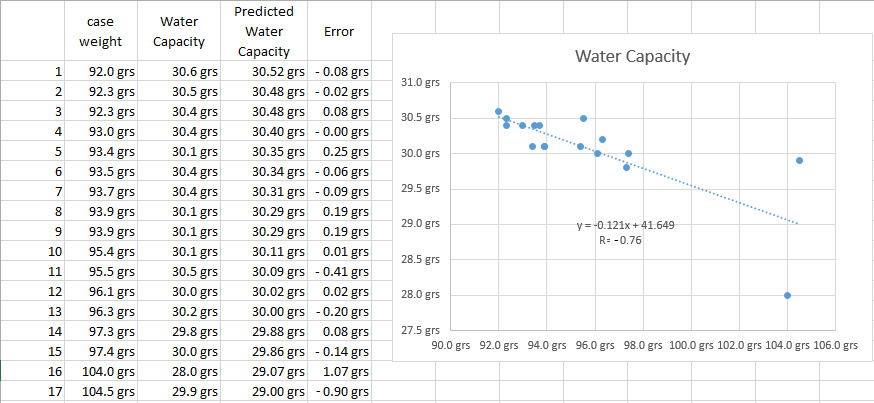
Steve 4102, I looked at the table you mention in post #13 that is linked in post #2. I believe it shows clearly that as case weight goes up, case capacity goes down.

It also shows clearly that the two are not locked together in a way that is terribly useful to the discerning handloader, so I do take your point. Measuring the primary object of your attention (capacity) is always superior to measuring a proxy (case weight).

I wonder if the O.P. weighed the brass with primers in place (probably, else the water would leak out) and if primer weight makes much of a difference? I also wonder if the cases were sized and trimmed before the water capacity was determined? How much care was taken to ensure temperature was controlled and air bubbles prevented? Was powder reside inside the cases a factor?

These are just the wrinkles in the measuring process I could think of immediately.

Just covering all the bases, I am,

I guess we are not looking at the same chart.

Here is the link again.

http://www.6mmbr.com/223rem.HTML

Right off the bat with #2 and #3,

WCC99 weight=95.5, Capacity=30.5

S & B Weight=92.3, Capacity=30.5

Same capacity different weight.

Another example,

Federal weight= 96.3, Capacity=30.2

Hornady weight=93.9, capacity=30.1

In the above, the federal case weighed +2.4gr+ more than the Hornady case, yet the Federal case had .1gr More capacity.

 

[Lost Sheep]

I copied the data from the chart (yes, we are looking at the same one) into a spreadsheet (EXCEL) and created a scattershot graph. Then eyeballed a line through the data. There is clearly a trend.

There is also apparently enough "scatter" away from the line that the relationship between case weight and case capacity is not tight enough to be useful to the critical handloader. But to say there is NO relationship is just as apparantly incorrect. It is just not a relationship that has a lot of use to us. (I hope I did not misinterpret your posts.)

Lost Sheep

Sorry I can't figure out how to actually insert the image right into the text. I have done it before, but, for me, it is an iffy proposition.

 

[Metal god]

I still have a hard time excepting that case weight has NO correlation to case capacity . You all are talking about a pretty small case and not a whole lot of weight difference . Sure it's a large-ish percentage of weight but Not enough the make a difference in such a small case . I know there can be as much as a 30gr difference in a 308 case and would assume even larger cases can have even a bigger difference . Are you saying a 30gr difference in case weight in a 308 case will have NO effect on case capacity ?? I don't by it . IMHO , making a blanket statement that case weight has no effect on case capacity is inaccurate .

 

[Lost Sheep]

Metal God (post 23), that is what I am saying.

Brass has a specific gravity of about 8.5 (which can vary a bit). That means for every 8.5 grains of extra brass in a case, you lose 1 grain of water volume capacity. There's the relationship and close to the (mathematical inverse) of the slope of the line I drew on the graph I attached to post 22)

Lost Sheep

 

[Metal god]

lostsheep :

Yep I understand and did look at your graph , my post was not directed at you but rather just pointing out that in general 10gr or less difference will not likely effect the ballistic . Sure some but IMO you would need a much bigger sample then a few shots , 10 at minimum . How ever a rather large difference in case weight will effect ballistics .

 

[Unclenick]

Lost Sheep is correct. I did the same thing he did, but I rearranged the data in decending order of the brass weight to make the comparison more intuitive (to me, anyway) and showed the least squares fit equation and then the amount of error it makes. In 8 of the 17 instances, the formula predicts the water capacity of the cases from their weight to within 0.1 grains. The worst case if for what is case #16 on my list, for which the formula prediction is off 3.8%. The correlation coefficient is -0.76. It would be -1.00 if the formula predicted the water capacities perfectly accurately and every weight was on the line. It would be 0.00 if there were no correlation at all.

So, why isn't the fit perfect? Two reasons. One is that not all brass is made from the same alloy, as this article shows. Therefore, the density of the brass isn't the same. In the main, the brass runs the gamut from 80:20 Low Brass to 60:40 Muntz Metal, with 70:30 Cartridge Brass in the middle. From Matweb.com, the differences in densities are:

Copper:Zinc / Density at 68°F /     Name

60:40       /  8.39 gm/cc     /  Muntz Metal
70:30       /  8.53 gm/cc     /  Cartridge Brass
80:20       /  8.67 gm/cc     /  Low Brass

The second reason is the head dimensions don't match. A head may have more or less diameter, or more or less rim thickness, or a more or less acute extractor groove relief angle. All these features have tolerances, and when you add metal at the solid part of the head through increased diameter, or increased rim thickness, or shallower extractor groove relief angle, it increases weight without affecting the capacity of the case body in front of the head.

Back in the 60's or 70's, Wm. C. Davis determined that if you have a case that is about 16 grains lighter, it requires you increase powder charge 1 grain to keep pressure constant. It is an approximation that is affected by the scatter in the prediction formula, but if the head dimensions match, I've played with this in QuickLOAD, which basically agrees, finding a range of between 14 and 16 grains, depending on the powder and case. Davis did the experimenting with .30-06, but it is a surprisingly consistent relationship over many chamberings. Figure that for 70:30 cartridge brass, an average value is about –1.8 grains of water capacity difference for each grain of powder charge increase.

 

[steve4102]

Here is a prime example of why there is no direct correlation between case weight and case capacity of different headstamps.

Note the obvious difference in case head diameter.

 

[Metal god]

Here is a prime example of why there is no direct correlation between case weight and case capacity of different headstamps.

Oops , I missed the part you all were just talking about headstamp differences . I thought this was just about comparing case weight to case volume and headstamps were not included . I would agree if a Winchester and Federal case both weigh 95gr . That does not mean they both will have the same water capacity .

Note the obvious difference in case head diameter.

I don't see what you're talking about . What is the caliper measurements ? I'm not sure what you mean by diameter , what should I be looking at . I'm having a hard time seeing a difference because one case has a primer in it and it seems to give an illusion of difference to me .

 

[hartcreek]

But doig the water meathod u also have the problem of different primer having different capacities because of the primer design and wall thickness let alone your ability or lack there of to vent all the air as this will effect what you are able to measure. The problem is that 5.56 cases are so puny in the first place that brass composition can make a big weight difference.

I am staying with weighing my cases and seperating by headstamp but I still do a volume check with powder with my heaviest cases just to be certain when wporking up a load.

 

[jwrowland77]

But doig the water meathod u also have the problem of different primer having different capacities because of the primer design and wall thickness let alone your ability or lack there of to vent all the air as this will effect what you are able to measure. The problem is that 5.56 cases are so puny in the first place that brass composition can make a big weight difference.



I am staying with weighing my cases and seperating by headstamp but I still do a volume check with powder with my heaviest cases just to be certain when wporking up a load.

I take the old primers out....first. I use a plug that weighs the same every time so the only difference is going to be in the case.

Not to mention, even if you used the primer. The same primer is going to weigh the same both times you weigh it. You weigh once without water, and once with. Same primers weight gets accounted for both time, so still, the only difference is in the water capacity.

 

[FlyFish]

Here is a prime example of why there is no direct correlation between case weight and case capacity of different headstamps.

As Unclenick's plot, and particularly the correlation coefficient (r) show, there clearly is a direct (technically, an "indirect" - as case weight goes up, capacity goes down) correlation between case weight and case capacity, and it's highly statistically significant at p<.01, meaning there's less than 1% chance that there is in fact no relationship and the results seen are occurring only due to chance. I think what you really mean is that the correlation isn't perfect, and it isn't - if it were, the r value would be 1.00 and all the points would fall on the same line in the plot.

The value r^2 (r squared) is known as the coefficient of determination, in this case -0.76^2, or .5776. That means that about 58% of the variability in case capacity can be "explained" or predicted by the case weight, leaving the other 42% due to other (currently unknown) variables and "error" which is a statistical term for randomness. I think Unclenick did a good job of identifying what some of those other variables might be and it would be possible, theoretically at least, to expand the table with additional columns containing measurements for them and then evaluate the relationship as a polynomial regression, which would allow each of those other variables to be ranked in terms of the amount of additional variability (i.e., the 42%) they account for.

 

[jwrowland77]

I'll have to test out my Win and Hornady brass in my .308. There's 10gr difference in weight, same exact capacity.

Hypothesis: they'll shoot exactly the same since capacity affects internal pressures, which should give close to same velocities and shoot just as accurately.

The point is, if you have consistent capacities, you'll get consistent results, which help at 600 and 1000 yard mark.

 

[higgite]

I think it’s safe to say that in a batch of single headstamp brass, the lighter ones will hold more water than the heavier ones. But, start mixing headstamps and it becomes a crap shoot, as witnessed by the table in Steve’s link and Unclenick’s and Lost Sheep’s graphs. Especially Nick’s chart where the differences between “predicted” and actual water weights bounce around from plus to minus. Two cases of the same weight but different headstamps are more likely than not to hold different amounts of water. If someone is going to go to the trouble of sorting cases by weight, hopefully they have already gone to the trouble of first sorting them by headstamp.

 

[Jim Watson]

Interesting, but I am not going to be sorting range pickup by weight or volume for target shooting, so the lack of perfect correlation with different brands of brass does not matter.

Has anybody taken several of the same lot number and compared volume vs weight?

I sorted 500 of the same lot number WW .223 into batches of 94.x and 95.y. that got me two sub lots of over 200 each. The <94.0 and >95.9 cases were few in number and went into the plinking stock.

I once read a rule of thumb that a change in case weight of 11 grains called for a one grain change in powder charge. I had not seen the Davis number of 18.

 

[wogpotter]

Different caliber (.303 British), but these are some results of a test I did a while back.

Brand	Weight	Volume
S&B	183.7	57.1
S&B	184	56.3
S&B	184.6	56.8
S&B	184.5	53.2
S&B	166.3	56.5
		
PPU	181	55.6
PPU	183.1	56.5
PPU	184.4	56.1
PPU	183.1	56.1
PPU	180.3	53.4
		
REM	161.7	54.5
REM	161.3	53.7
REM	162.2	55.5
REM	159.8	55.5
REM	160.2	53.8
		
WIN	168.1	53.8
WIN	167.8	52
WIN	168.1	53.6
WIN	168.2	54.7
WIN	167.8	52.3
		
HXP	186.7	53.8
HXP	177.1	53.3
HXP	185.7	53.6
HXP	185.2	54.5
HXP	188.4	53.7

 

[Unclenick]

Here is a prime example of why there is no direct correlation between case weight and case capacity of different headstamps.

The problem with your statement is the word "no". That's mathematically incorrect, as I demonstrated with the .223 data in Excel, where the correlation coefficient is R=–0.76. For "no" correlation, R has to be zero, as in the top middle row of the image below. So there is a correlation between brass weight and capacity, it just isn't exact and has outliers.

I think maybe what you are trying to say is the correlation isn't strong enough to base load adjustments on unless you are working with the same headstamp, and I think that's generally true, and even where it isn't, as with the 8 .223 cases in the data for which the predicted water capacity was very close, I wouldn't just assume I'd be able to get away with that without first testing it on enough samples to be confident I could. It's analogous to the way there is a correlation between CUP and psi, as Denton Bramwell showed, but its just not a good enough correlation to base calculation of a target load pressure limit on.

I think perhaps the confusion is in not being familiar with correlation occurring in degrees. Below is an image I derived from a Wikimedia Commons image file by Wikipedia user DenisBoigelot, and posted in the Wikipedia article, Correlation and dependence. The top row shows correlation coefficients from 1 to –1 in 0.2 size steps. The second from right is –0.8, which is very close to what the .223 brass exhibited, except the illustration is based on the scatter having a random normal distribution, where the brass has a non-normal distribution imposed by forming die design. The second row contains additional examples of where the correlation coefficient is either 1 or –1. I think that's the kind of correlation you had in mind, but that's a perfect correlation, which doesn't happen even with the same headstamp brass; not that exactly. The cropped part is a collection of zero correlation plots of the kind a mathematician finds interesting, but not anything we'll see with brass.

 

[4runnerman]

This is very intresting. If case weight makes no difference, Why do all the top bench shooters sort their brass?. Some will buy 500 cases to get 100 that weigh the same. I find it hard to believe that they are doing it just because. My 223 brass,I do not worry to much about. I will use brass that comes in between 72 and 75 gns. The rest I sell. JW- Your tests, While that is some very good shooting-With the case weight difference can you for sure say it's the case that made the issue or is there human error involved?. While I do somewhat believe that small weight difference does not affect to much,Im sure it does as the weight gets to be more.

 

[jwrowland77]

True very true. I see where you're coming. I guess the only true way to know would be to have a remote trigger puller to keep from any human interaction. I could have shot from a lead sled but I actually feel more comfortable shooting from a bipod and rear bag now. Lol

I'll probably end up running the test again just because that's me. Lol

 

[Unclenick]

4runnerman,

Sorting by weight doesn't necessarily find case capacity. The drawing below is from something I actually did with some bulk Winchester .308 Win brass I bought, which was to take coarse grid layout paper (Walmart caries it in big sheets with half inch grid as Ghostline posterboard), and mark the weight range divided into 10ths of a grain on the grid bottom (you have to weigh some samples to find the range first), then stack all the cases with each weight above it's marked position. This forms a weight histogram of the cases.

As shown below, there are peaks that suggest the brass weight range is comprised of four independent normal distributions, suggesting the brass is the mixed product of four different tool sets. So, weighing tends to get you brass off the same tool set if it's near one of the peaks. Usually one tool set will turn out to produce a little bit better concentricity than another, which helps with bullet alignment in the chamber. There may also be variations in exact hardness or other brass properties that it could help to minimize inconsistency.

 

[jwrowland77]

I found this same trend weighing Lapua when I first started shooting comp and caring about my precision reloads. Where brass would be tight around three different weights.