MightyMO1922,
The correct answer to your question is no, if I take “directly related” literally in the mathematical sense, meaning a proportional relationship between the two. If you’ll bear with me, I’ll see if I can specifically address what you are asking about.
When you fire a gun, some portion of the energy stored in the powder is converted to kinetic energy in the bullet. The bullet’s kinetic energy is equal to the amount of work that went into accelerating it (the units of work and energy are the same). It is equal to the force applied to the bullet multiplied by the distance the bullet traveled in the direction of that force while under its influence. This is why one unit of kinetic energy (and work) is the foot-pound. A thousand pounds of force applied for two feet of bullet travel will give you a bullet with 2000 foot-lbs. of kinetic energy. When the force varies, the energy it imparts equals the product of the average force and the distance over which is was applied.
Since kinetic energy may also be found as half the bullet mass multiplied by the square of its velocity, it follows that the average force applied to the base of a bullet during its acceleration is proportional to the square of the velocity of the bullet, and not directly to its velocity. So you can square whatever velocities you have and judge the variation in average force on the bullet base from that. Since the average force on the bullet base is equal to the average pressure behind the bullet divided by the cross-sectional area of the bullet, it further follows that variation in the square of velocity is proportional to average pressure in the barrel. But this is the average pressure; not the peak pressure.
Below are exaggerated pressure and velocity curves for fictional fast and slow powders to illustrate the principle involved. Firing the same kind of bullet, the areas under the red and the blue pressure curves are the same, so the average pressure for both curves are the same giving the same muzzle velocity and therefore the same kinetic energy to their identical bullets. But you can see that the peak pressures are different. The slow powder cannot burn fast enough to keep up with the bullet, so the peak pressure is lower. Indeed, it takes a heavier charge weight of the slow powder just to get enough powder burning to keep up as well as it did. But even if it makes gas slowly, the heavier charge weight makes a larger total volume of gas, so pressure does not drop off as quickly as the bullet proceeds down the bore. That extra pressure late in the bore is why it can get to the same final velocity as the faster powder with the higher peak pressure did, and therefore produce the same kinetic energy, even though the peak pressure was lower.
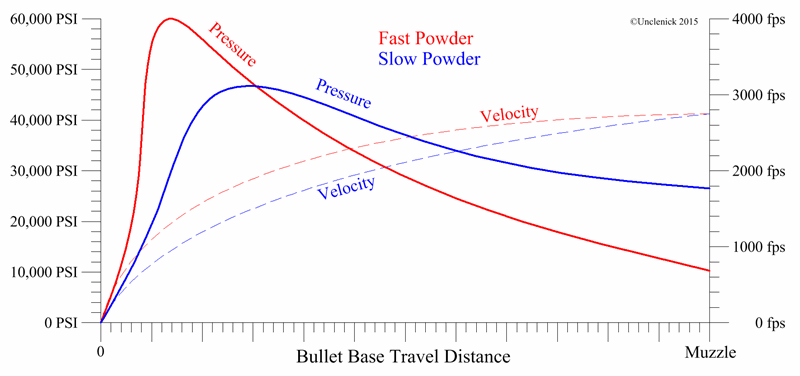
Note that there are a couple of consequences to selecting powder burn rates. Because the heavier slow powder charge has more mass and because the pressure at the muzzle is higher, it will have more “rocket effect” from accelerating that greater gas mass with higher pressure after the bullet clears the muzzle. This produces more recoil.
Another consequence is that because the slow powder imparts velocity to the bullet more gradually, the bullet takes longer to get to the muzzle from the start of the powder burn. That longer barrel time means the muzzle won’t deflect to the same position that it did with the faster powder, so the POI can be significantly different for the two loads, even though velocity is the same.
A third consequence is if the bullet is too light for the powder burn rate, it can actually get so far ahead after the peak that the pressure that it doesn’t accelerate as fast as the powder mass, so the mass of the gas slams into it and creates a local high pressure zone at the base of the bullet. This can ring barrels, or in very extreme cases, bulge or even blow the muzzle off a barrel. Unfortunately, the only way I know to if this is happening is with a strain gauge pressure measuring system, because that lets you see the resulting transverse wave in the steel surface when it reaches the chamber, making it look as if there were secondary pressure spike at the chamber, when there isn’t actually any pressure produced there.
With permission from Jim Ristow at
RSI:
On the other hand, the fast powder cannot be loaded to as high a velocity as the slow powder can before it exceeds the peak pressure limit. Even more slow powder can be put in (assuming it fits) raising the average pressure and velocity with it, before it exceeds the peak pressure. Note that this also means that if you have a “fast barrel”, one the same length as the data test barrel, but that gets faster velocities than the test data, which is uncommon but occasionally occurs, it means loading up to the point of matching the published maximum velocity will actually put you over the maximum pressure published for the test gun.
Finally, if you want to estimate what a load is doing in your gun, there is a complicated way to go about it. Mehavey suggested peak pressure varies the cube of velocity, but that’s only an average sort of relationship because the actual number varies with the progressivity profile of the powder and also with barrel length and bullet weight. You can discern the exponent for any particular choice from published test gun velocity and pressure measurements such as Hodgdon has for their barrel length. For medium power rifles with 24” barrels it will usually be within a range of 2.5 to 3.5. But you can, especially with pistol powders and barrel lengths, find smaller exponents.
Where:
P1 is the starting load pressure
V1 is the starting load velocity
P2 is the maximum load pressure
V2 is the maximum load velocity
Epv is the peak pressure exponent with velocity
Epv = log(P2/P1) / log(V2/V1)
You can also find a pressure exponent for the powder charge by substituting the starting and maximum powder charges for the starting and maximum velocities. The result will be close to the same because velocity goes up pretty linearly with powder charge, except the powder exponents will usually be around 10% or so lower because the pressure curves hook over some by the time they get to the usual starting load to maximum load range. This is worse with CUP than with psi because of non-linearity of the copper crushers at higher pressures. Velocity or powder charge change can be used to predict pressure using their own exponents, and the numbers may be used to determine what pressure a change in velocity or powder charge will produce
in the data source’s pressure test gun,
but not in your gun, except by analogy.
Determining pressure for your gun is more complicated for several reasons. It requires, as mentioned earlier, that your chronograph is as accurate as the one the load data development used. Actual chronographs, according to Bryan Litz, cannot normally be trusted to be more accurate than about 15 fps. And that’s a good one. Finding a cheap one off by 50 fps is not unusual. I’ve personally seen one off by 200 fps in late afternoon lighting conditions. I know that because we had an Oehler 35 P running next to it that didn’t mind those same afternoon light conditions and gave 200 fps slower readings (which was more reasonable for the load in question).
Other mechanical issues can affect the result in your gun, such as you having bore condition with different friction, or having unven bolt lug contact so there's some added chamber shape stretching, etc.


