It will be closer to 2.5 grains to make the pressure match, and probably just closer to 2.25 grains to get the velocity to match.
You do need to understand a little basic physics here. On the plus side, if you don't like physics, this is pretty easy when you are just trying to get a velocity match from two guns with the same barrel length using the same bullet and powder and case and primer in the same chambering.
Note that most SAAMI pressure barrels are 24", so if you compare a 26" barrel's velocity to published pressure and velocity data, you have to allow for that difference.
At any given instant, the force pushing the base of the bullet in a gun barrel is the value of the pressure at its base divided by its cross-sectional area. When the force is high, acceleration is high and vice versa, but final velocity is the net result of the acceleration that occurs all the way down the barrel, and not just at the peak, which is why velocity does not give you a peak pressure number.
In physics, the concept of work is just force times distance. In English units, it is the distance in feet times the pounds of force that applied to move an object, so the unit of work is foot-pounds. In SI metric units it is newtons of force times the meters of distance over which that force is applied, so the unit of work is the newton-meter.
You may have noticed the English unit of work is the same as the English unit of energy: the foot-lb. Similarly, in the SI units, the newton-meter is a measure of energy equal to one joule. Indeed, when you look at projectiles, the kinetic energy they carry at the muzzle is exactly equal to the work put into moving them down the length of the barrel. For that reason, some like to think of kinetic energy as stored work or potential to do work. It is always equal to the amount of work the bullet can do parting the air and acting on its target.
When you calculate the kinetic energy of a bullet, it is the square of its velocity times half its mass. It turns out the velocity in that equation is the exact velocity the work equal to that kinetic energy will bring the bullet to when it reaches the muzzle.
So, if you have two bullets the same weight, and they reach the same velocity in the same length of barrel, the average force and therefore the average pressure behind them in these barrels must be the same, discounting any difference in friction. However, peak pressure is not average pressure. The peak pressure need not match in that situation, as explained next.
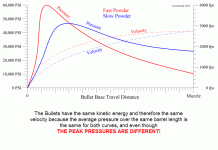
Below is a plot of two different powders producing the same velocity in the same barrel length. One is a fast powder; one is a slow powder. The slow powder has a heavier charge weight that produces greater total gas volume. That is why it keeps the pressure in the barrel up higher later in the bullet's travel. Because that higher late pressure provides more late barrel acceleration than the faster burning powder does, it makes up for producing lower acceleration at the pressure peak.

So, velocity and barrel length tell let you deduce average pressure in the barrel but not a peak pressure value. Peak pressure is the one that is critical for safety. But what about the situation where you have the same chambering, the same case, primer, and powder and barrel length, but it takes more powder in one gun to reach the same velocity the other gun does with less powder? Well, like the slow powder in the example, above, the larger charge will produce higher late barrel travel and muzzle pressure that make up for acceleration not present at the pressure peak. So, the peak pressure in the gun requiring the heavier charge will be lower.
Any time you need more of the same powder to reach the same velocity from the same barrel length in a second gun with the same barrel length, the peak pressure in that second gun will be the lower of the two at that velocity. That is so, regardless of whether the extra powder was needed because your case capacity is greater or because your primer is weaker or because your gun's dimensions are just loose. But, conversely, if you need less powder to reach the same velocity with the same bullet in the same barrel length (say, your case had much less capacity than the original test case did), then you have higher peak pressure than was present for the databook author's load measuring.
One may be tempted to try to translate this to other chamberings. Note that other chamberings typically have different case lengths, and since barrels are measured from the breech face, bullets from, say, a 30-06, have a little less bullet travel in a 24" barrel than a 308 Winchester does. So keep the different barrel lengths in mind. Be sure you know how to extrapolate velocity difference from a different barrel length. QuickLOAD does this best, but you do have to tweak the arguments to get its output to match measured pressure and velocity from the factory data first. Absent measured load data to compare it to, you must, for safety reasons, assume it has an error margin and treat it only as an estimate.