Yep. I did the same thing awhile back. I made up an Excel file that "shoots" random groups in order to keep actual shooter and gun bias out, but the results weren't very different in this example except that I "fired" the shots a number of times so that the extreme size difference in the two groups of three came close to the 95% confidence limits. So this isn't likely to happen every time, but will happen roughly one time out of twenty or so.

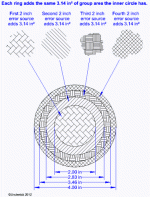
The older image below plots upper and a lower limits for group sizes at the 95% confidence range. I took it from tables in the Lyman #47 Handbook's article on stats for shooters. The vertical height between the blue and red lines is how far the group sizes would range 95% of the time if the average size were one unit of you choice (inches, moa, cm, etc.; the green line). You can see 25 shots give you about half the error range that ten shots do. The propensity to err (miss the point of aim) remains the same, but as the group size grows, so does the overall size of the group, causing that propensity's contribution to be smaller relative to the overall size of the group 95% of the time. This is because the more rounds you put in each group, the bigger the group gets. That's due to offering the lower likelihood errors more opportunities to occur, increasing the liklihood that they will.

The other problem shooters have is that standard deviations of different error sources contributing to the overall size of a group add together as the square root of the sum of their squares. In other words, suppose you have one source of error, like cast bullets with inclusions that unbalance them, that cause random 2 moa error in a 30 round group fired from what is otherwise a perfect one-holer gun. Then you fix that error, but create another one, like a loose scope reticule, that also produces 2 moa of random error. Most folks think that if you combine both errors at the same time you will get 4 moa groups, but you won't. Because the sources are both random and not synchronized as to either direction or magnitude, they don't actually add like that very often. Average groups will be about 2.8 times bigger (the square root of the sum of the squares, √(4+4)=√8=2.8…). So, the shooter who has had both problems all along can be forgiven, when he discovers just the scope problem and corrects it, of thinking it wasn't that big a deal, because average groups only come down from 2.8 to 2.0 moa. Plus, if he is shooting small group sample sizes, like 3, he will have so much scatter from the small samples that he may not see any improvement at all, even though he's actually removed half the problem.
Note that the area of a 2.8… inch circle is exactly twice the area of a 2" circle, so you can think of each error source as adding its isolated area to whatever set of problems you incorporate it into. The bottom line, though, is until you get down to the last big source of error, correcting it doesn't appear to have made a major difference to the overall size of the group. It would, however, improve your score over the course of an 80 round NRA Highpower match. That is because you will randomly get more scoring ring scratches even with a small diameter change in the overall group. So, fixing any source of error is still worth it from the perspective of target scores.
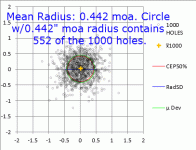
Lastly, here is a 1000 shot group with the group size evaluated by several measures. Note that as the group size gets large, the difference in results aren't great. So you can pick your poison in terms of such evaluations. (Mean radius is μDev below (green circle))