Flat nose bullets have enjoyed increased popularity over the years. I'm sure Elmer Keith, who designed the SWC, would disagree about it being no better than a round nose, but his SWC designs had a pretty wide meplat (the flat area of the tip), and I don't think he would disagree about the killing power of the still wider LBT designs popular today.
The problem with expanding bullets has always been that compromise or trade-off between penetration and destructiveness. Rifles have enough power so that the expanded cavity is partly permanent, so they are usually pretty effective in rifles as long as you stay within the bullet's terminal velocity design range. But many folks
swear by a blunt solid as it also widens the wound channel but has a greater chance of extending that channel clear through and creating an exit wound. At handgun power levels the problem is greater because there is less energy to spare and the temporary cavity gets a lot of that energy while only sometimes shocking the target with it. Other times the handgun's temporary cavity doesn't seem to do more than make the target mad. That response is unpredictable, but is the reason more emphasis is put on penetration in newer designs. But in all cases the temporary cavity's energy drain does reduce maximum penetration. So the blunt solids have a good following in the midst of that whole debate.
It isn't weight, but sectional density that determines acceleration by pressure. Sectional density (SD) is how much mass you have for each unit of cross-sectional area. In a gun, that cross-sectional area is the area of the bore opening. And since the force provided by a given pressure also increases with area, a constant sectional density means each unit of force is acting on the same amount of mass. That's keeps acceleration constant. If you double the cross-sectional area of the bullet and also double the weight, the same pressure will make double the total force and accelerate the doubled weight at the same rate as the single weight was with the same pressure on the original amount of area. But if you double the weight by making the bullet longer and leave the cross section area and pressure the same, then acceleration will be cut in half because each unit of force now has twice as much mass to accelerate.
A ballistic coefficient is a number that tells you how gradually your bullet is slowed by drag. There is more than one kind of BC, but for all kinds, the higher the ballistic coefficient is, the more gradually the bullet slows down as it flies through air (or goes through other media, as you discovered). You can get the physics or aerodynamic version of a ballistic coefficient by dividing the sectional density of the bullet by its drag. The drag is normally calculated from the factors that cause drag in all things moving through a fluid multiplied, then is adjusted by multiplying by a drag coefficient that was measured for the actual bullet shape. Basically, the higher the sectional density (SD) of the bullet, the more force it takes to slow it down at a given rate. As a result, when you calculated BC, SD is in the numerator while drag is in the denominator. For a given bullet nose and tail form, higher SD means higher BC, and higher drag means lower BC.
In ballistics only, there are two things to be aware of: One is that the ballistic SD of a bullet is not it's physical SD, as it was in the aerodynamic calculation. In ballistics it is a convention to use the area of a square the diameter of the bullet rather than the actual circular cross-sectional area. Because bullets are normally circular in cross-section, the error is always of the same proportion and the comparative SD and SD-related behavior of any two bullets remains accurate. Using the area of the square, D², simplifies the calculation by eliminating the need to calculate ϖr². This shortcut was devised because field artillery officers were asked to make the calculation in combat real time (this was before computers) and any step that saved time might be critical for them. That is now an obsolete concern, but the habit of using the shortened calculation remains.
Second, because of that proportional SD being accurate only in making comparisons, the BC used in ballistics is based on comparing your bullet to a reference projectile for which the SD is calculated the same way and for which velocity loss tables have been compiled from actual firing measurements. This also saves having to make very complicated fluid dynamics calculations near the speed of sound, where drag jumps up quickly due to the start of shock wave formation. Instead, you just divide your bullet's ballistic SD by the reference projectile's SD to get the BC, which is the comparative rate at which your bullet will be slowing down when it is flying at the same speed in the same atmospheric conditions. The reference projectile tables are adjusted so the reference projectile has a ballistic SD of 1.0 and a BC of 1.0. This further simplifies the calculation because then your BC is just equal to your SD,
provided your bullet has the same shape as the reference projectile.
Well, usually your bullet is not the same shape as the reference projectile. As a result, a shape difference correction factor has to be added in. It is called the form factor or form coefficient,
i. So BC then is:
Your bullet ballistic SD / (
i × Reference projectile ballistic SD)
Since the reference projectile SD is always 1.0, this simplifies to:
BC = Your bullet ballistic SD /
i.
Now there is one last complication. There is more than one shape of reference projectile, and the closer the shape of your bullet is to the shape of the reference projectile, the closer
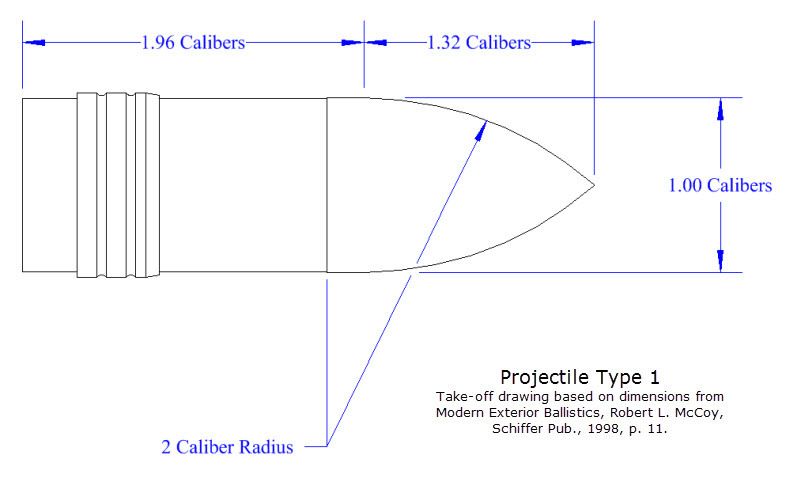
i is to 1.0 and the closer your BC is to being simply equal to your ballistic SD. The most common reference is the Type 1 reference used in firings to create the Gavre Commission table of 1917. Because it was tabulated by the Gavre Commission, it is called the G1 reference projectile. The original projectile used in these firings and before adjusting the tables for an SD of 1.0 and a BC of 1.0, it was an artillery shell that looked like this:
You may well ask how closely this projectile resemble the bullet you actually have. For some pistol bullets, it is too pointy. For most rifle bullets that are not round nose, it is too blunt. It is about right for a lot of cast rifle bullets. They are often longer, but added length alone doesn't have a big effect on drag.
For those bullet for which the shape is a poor match, there are other projectiles to reference to. To honor the Gavre Commission, even though most of these shapes were come up with by the U.S. Army Ballistics Research Lab, the prefix letter G still attaches to the rifle bullet shapes. These other reference projectiles range from a round ball and a straight cylinder (like your wadcutter) to very sleek long shapes that match a VLD bullet. Obviously a long sleek projectile will slow down more gradually, so if you use that shape as your reference, the BC's you get from it will be smaller numbers because the
i will be larger. For example, a pointed rifle bullet might have a G1 BC of 0.45, but the same bullet as compared to the long, pointed G7 reference projectile will slow down comparatively faster and will thus have a G7 BC of just 0.222.
So, why do we care about BC's? Well an obvious reason is a larger BC means a bullet will fly further and arrive at a given distance faster. That means you have to lead a moving target less and wind will have less time to affect it. But the main reason most of us want these numbers is that they provide a compact piece of information that velocity and drop and windage tables may be calculated from. Ballistics software can take a BC and generate these tables for you. It turns out that the closer the shape of the reference projectile is to the shape of your bullet, the more accurate those tables are, though the difference is usually small enough that it matters only to long range riflemen.