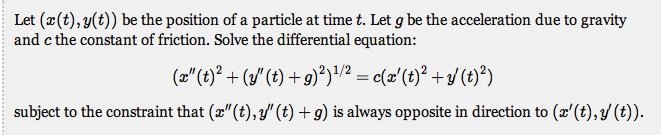In how to calculate exactly the path of a projectile under gravity and subject to air resistance should be of interest to the firearm community. That is one smart teenager.
Read more: http://www.foxnews.com/world/2012/0...r-isaac-newton/?intcmp=obinsite#ixzz1wAqUJ26G
Read more: http://www.foxnews.com/world/2012/0...r-isaac-newton/?intcmp=obinsite#ixzz1wAqUJ26G